Understanding the Median Filter: A Powerful Tool for Noise Reduction in Image Processing

In the fast-paced world of digital imagery, where images are captured, transmitted, and processed at an unprecedented rate, ensuring high-quality visual data is essential. However, this pursuit is often hampered by the presence of unwanted noise, which arises from various sources such as sensor limitations, transmission errors, or environmental factors. Noise can degrade image quality, obscure critical details, and impede accurate analysis, making it a significant challenge in image processing and computer vision.

Fortunately, there are several techniques available to combat noise, and one particularly powerful tool that has stood the test of time is the Median Filter. The median filter is a popular and effective method for noise reduction, offering unique advantages over traditional filters like the mean filter. Its ability to preserve edges and fine features while efficiently suppressing various types of noise makes it a cornerstone in image processing applications.

In this post, we will delve into the inner workings of the median filter, exploring its fundamental principles, applications, and performance considerations. We will also examine different types of noise commonly found in images and their detrimental effects on image quality and analysis. By understanding the workings of the median filter and its underlying principles, we can grasp how this versatile tool can elevate the quality and reliability of digital imagery across various domains.

Whether you are a seasoned image processing enthusiast or a curious learner keen on exploring the intricacies of this powerful technique, join us as we embark on a journey to unravel the mysteries of the median filter. From its humble beginnings to cutting-edge variants, we will explore the diverse applications and techniques that harness the median filter's potential to transform noisy and distorted images into clearer, more informative representations.

So, without further ado, let's venture into the realm of the median filter and discover how this simple yet effective approach can bring clarity and precision to the world of image processing. Whether you seek to enhance medical images for accurate diagnosis or analyze satellite imagery for environmental monitoring, the median filter has a role to play in every pixel's journey from raw data to meaningful visual information. Let's get started!

The Basics of the Median Filter

The median filter is a powerful digital image processing technique used to reduce noise without blurring or degrading the sharpness of important image features. Unlike traditional filters, such as the mean filter, which replace each pixel's value with the average of its neighbors, the median filter takes a different approach. Instead of using a statistical mean, the median filter calculates the median value within a local neighborhood, effectively removing outliers and preserving valuable details in the image.

Definition and Concept

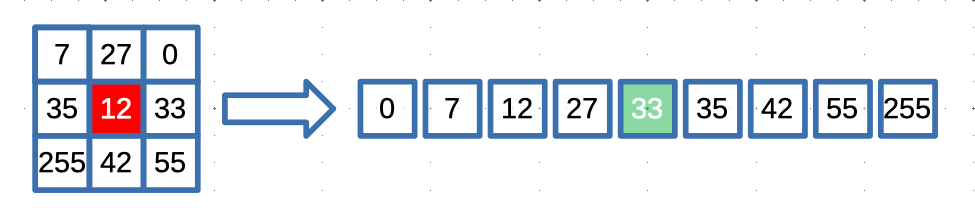
The median filter operates by considering a sliding window, also known as a kernel or mask, which moves across the image pixel by pixel. At each position, the pixel intensities within the window are sorted, and the median value is chosen as the new intensity for the central pixel. The median value is the middle value in a sorted list of pixel intensities and is robust against extreme values, making it an ideal choice for removing noise.

Advantages over Mean Filter

One of the key advantages of the median filter over the mean filter lies in its ability to preserve edges and fine details. In the presence of noise, the mean filter tends to blur edges and contours, whereas the median filter efficiently suppresses noise while retaining the sharpness of image boundaries. This characteristic makes the median filter particularly valuable in applications where preserving important structural information is crucial.

Handling Salt-and-Pepper Noise

Salt-and-pepper noise, characterized by randomly occurring bright and dark pixels, can severely impact image quality. The median filter is particularly adept at handling this type of noise, as it replaces noisy pixels with the median value, effectively discarding the extreme noise values without altering the overall appearance of the image.

Window Size and Impact

The choice of the window size (also known as the kernel size) is essential in the median filtering process. A smaller window size will be effective in reducing fine, localized noise, but it may also risk removing important details. On the other hand, a larger window size can better suppress broader noise patterns but might lead to blurring of the image. Striking the right balance between noise reduction and detail preservation is crucial and depends on the specific application and characteristics of the noise.

Robustness to Outliers

One of the significant strengths of the median filter is its robustness to outliers. In the presence of sporadic extreme noise values, such as those found in salt-and-pepper noise, the median filter disregards these outliers when calculating the median value. Consequently, it can handle noise that would otherwise disrupt the performance of other filtering techniques.

Application Areas

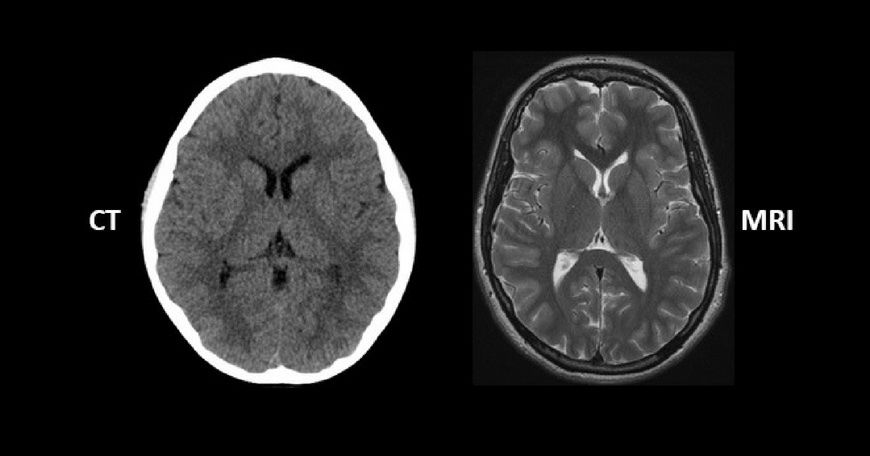
The median filter finds applications in a wide range of fields, including medical imaging, remote sensing, surveillance, and computer vision tasks. In medical imaging, for instance, it is used to enhance MRI and CT scans, ensuring accurate diagnosis and analysis. In satellite imagery, the median filter aids in noise reduction, improving the quality of data for environmental monitoring and mapping.

In conclusion, the median filter is a simple yet powerful technique that effectively reduces noise in digital images while preserving essential features and edges. Its robustness to outliers and its ability to handle various types of noise make it a valuable asset in image processing applications. However, it is essential to consider the trade-off between noise reduction and detail preservation by choosing an appropriate window size for each specific use case. As we delve deeper into the world of median filtering, we will explore more advanced variants and understand how to optimize its performance in various scenarios.

Understanding Noise in Images

Noise in digital images refers to random variations in pixel values that can result from various sources during the image acquisition, transmission, or processing stages. Noise is an undesirable artifact that can significantly degrade image quality and distort the information contained within the image. Understanding the different types of noise commonly found in images is crucial for developing effective noise reduction strategies and selecting appropriate filtering techniques. Here, we explore some of the common types of noise encountered in digital images and their effects on image quality and analysis.

Types of Noise:

a. Gaussian Noise: Gaussian noise follows a Gaussian or normal distribution, and it is characterized by small random variations in pixel values around the mean. This type of noise is prevalent in electronic imaging devices and results from thermal fluctuations and electrical interference. Gaussian noise appears as a subtle, low-intensity graininess across the image.

b. Salt-and-Pepper Noise: Salt-and-pepper noise, also known as impulse noise, is a type of noise that affects individual pixels, causing them to have either very high or very low intensity values. This results in random bright and dark pixels scattered throughout the image, resembling grains of salt and pepper. Salt-and-pepper noise is often caused by transmission errors or faults in image sensors.

b. Shot Noise: Shot noise, also known as photon noise, is inherent in digital images acquired with low light levels, such as astronomical or microscopic images. It occurs due to the discrete nature of light photons hitting the image sensor. Shot noise manifests as random pixel value fluctuations, which can affect image clarity and impact quantitative analysis.

d. Speckle Noise: Speckle noise is common in radar and ultrasound imaging, where it arises from coherent signal interference. It appears as granular patterns with varying intensity levels across the image. Speckle noise can obscure fine details and reduce image contrast.

Effects of Noise on Image Quality and Analysis:

The presence of noise in images can have several detrimental effects, including:

1. Loss of Detail: Noise can obscure fine details and degrade image sharpness, making it challenging to discern important features.
2. Reduced Contrast: Noise reduces the contrast between different regions of an image, making it harder to distinguish objects and structures.
3. Artifacts in Image Analysis: In quantitative image analysis tasks, noise can lead to inaccurate measurements and hinder reliable data extraction.
4. Adverse Impact on Compression: Noise can interfere with image compression algorithms, resulting in larger file sizes and reduced compression efficiency.
5. Degradation in Visual Appeal: Noise can negatively impact the visual appeal of images, making them appear grainy, blurry, or irregular.

The Role of Noise Reduction:

Noise reduction is a crucial step in image processing pipelines, as it helps improve image quality, enhances feature visibility, and ensures more accurate and reliable analysis results. The main challenge lies in removing noise while preserving important image details and structures. This is where filtering techniques like the median filter play a significant role, as they selectively remove noise without introducing significant blurring.

In the following sections, we will focus on the median filter and explore its effectiveness in reducing different types of noise while retaining the essential features of digital images. By understanding the behavior of the median filter and its application areas, we can gain valuable insights into how this technique can be harnessed to enhance image quality across various domains of image processing and analysis.

How the Median Filter Works

Understanding the inner workings of the median filter is key to grasping its effectiveness in suppressing noise without blurring or distorting the underlying image details. In this section, we will explore the step-by-step process of the median filtering technique and gain insights into its unique characteristics.

Step-by-Step Explanation:

a. Sliding Window Approach: The median filter operates using a sliding window or kernel, which moves across the image pixel by pixel. The size of the window is a critical parameter that determines the extent of the filtering effect. A larger window includes more neighboring pixels in the filtering process, offering better noise reduction but may risk blurring important details. Conversely, a smaller window size focuses on local noise reduction but might not be sufficient for suppressing broader noise patterns.

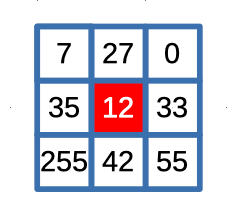
b. Pixel Sorting: At each position of the sliding window, the pixel intensities within the window are gathered and sorted in ascending or descending order. Sorting the pixel values is essential for finding the median value, which lies exactly at the center of the sorted list.

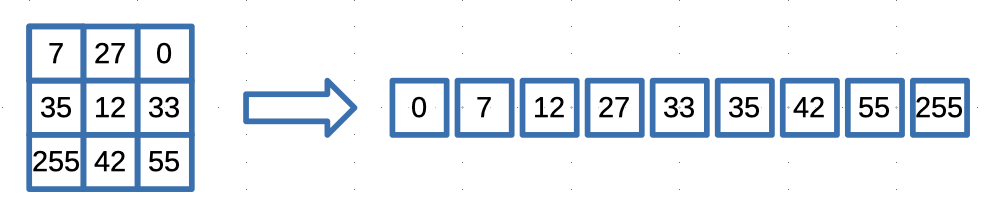
c. Median Calculation: Once the pixel values within the window are sorted, the median value is determined. For an odd-sized window, the median is the middle pixel value of the sorted list. In the case of an even-sized window, the median is calculated as the average of the two middle values. The median operation is robust against extreme noise values because it ignores outliers and focuses on the central tendency of the pixel intensities.

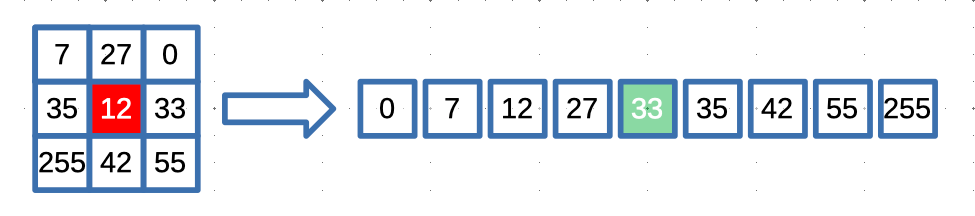
d. Replacing the Pixel Value: The median value calculated for the central pixel of the sliding window replaces the original pixel intensity. This process continues as the sliding window moves across the entire image, generating a new filtered image with reduced noise.

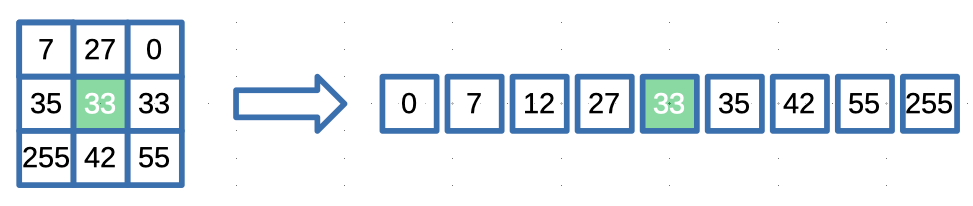
Preserving Edges and Fine Details:

Unlike traditional filtering techniques like the mean filter, the median filter is exceptionally well-suited for preserving edges and fine details in images. This is because the median operation effectively eliminates the influence of extreme noise values, which would otherwise blur the image boundaries. The median filter's selective noise reduction allows it to maintain sharp image edges, contours, and critical features, making it ideal for applications where preserving structural information is vital.

Handling Salt-and-Pepper Noise:

Salt-and-pepper noise, characterized by random bright and dark pixels, poses a common challenge in image processing. The median filter is particularly effective in handling this type of noise. When the sliding window encounters regions with salt-and-pepper noise, the median value will naturally fall between the bright and dark pixels, resulting in a smooth transition between the extreme values. As a result, the salt-and-pepper noise is effectively removed, leaving a cleaner and more coherent image.

Adaptive Window Size:

While a fixed window size is commonly used for median filtering, adaptive median filters exist to dynamically adjust the window size based on the local characteristics of the image. Adaptive approaches are beneficial in scenarios where noise characteristics vary across the image or in the presence of variable-sized structures.

By understanding the fundamental principles of the median filter, we can leverage this technique effectively to improve image quality, enhance feature visibility, and facilitate more accurate image analysis in various domains of image processing and computer vision.

Median Filter Applications

In this section, we explore some real-world applications where the median filter plays a pivotal role in enhancing image quality, improving analysis accuracy, and enabling valuable insights.

1. Medical Imaging:In medical imaging, high-quality images are crucial for accurate diagnosis and treatment planning. However, medical images are often affected by various types of noise, such as speckle noise in ultrasound images or Gaussian noise in MRI scans. The median filter's ability to handle different types of noise without compromising critical details makes it an invaluable tool in enhancing medical images. By employing the median filter, medical professionals can achieve clearer, more informative images, leading to improved diagnoses and better patient outcomes.

2. Satellite Imagery:Satellite imagery plays a vital role in applications such as environmental monitoring, land use classification, and disaster assessment. Images captured from space are susceptible to noise from atmospheric interference and transmission errors. The median filter effectively addresses these noise sources, allowing for more accurate analysis and decision-making based on cleaner satellite images. By reducing noise without distorting the landscape's intricate details, the median filter aids in monitoring environmental changes and identifying areas of interest with greater precision.

3. Digital Photography:Photographers often encounter noise in digital images, especially when using high ISO settings in low-light conditions. The grainy appearance of images due to noise can compromise their visual appeal. The median filter is a popular tool used in post-processing workflows to mitigate noise and restore image clarity. By applying the median filter selectively to noisy regions, photographers can retain the sharpness of important elements while achieving smoother and visually appealing results.

4. Video Processing:In video processing, noise reduction is crucial to improve video quality for various applications, such as surveillance, video conferencing, and entertainment. The median filter's ability to handle different types of noise, including temporal noise in videos, makes it an effective choice for video denoising. By applying the median filter to video frames, unwanted noise can be reduced, resulting in clearer and more pleasant viewing experiences.

5. Document Image Enhancement:In optical character recognition (OCR) and document analysis tasks, noisy document images can adversely impact text recognition accuracy and subsequent processing steps. The median filter is employed to remove noise and enhance the legibility of scanned or digitized documents. By reducing noise without affecting the text and structural details, the median filter facilitates more reliable and efficient document processing.

6. Image Restoration:In historical image restoration or digital archive preservation, the median filter can help improve image quality and visibility of aged or degraded images. By reducing noise and artifacts, the median filter assists in recovering valuable information from old photographs or ancient manuscripts, contributing to the preservation of cultural heritage.

7. Computer Vision Applications:The median filter finds applications in various computer vision tasks, including object detection, image segmentation, and feature extraction. By pre-processing images with the median filter, computer vision algorithms can achieve more accurate and robust results by operating on cleaner and noise-reduced data.

Performance and Trade-offs

While the median filter is a powerful tool for noise reduction in digital images, it is essential to consider its performance characteristics and potential trade-offs when applying it in various applications. In this section, we explore the computational aspects of the median filter, its effectiveness in different noise scenarios, and the trade-offs between noise reduction and feature preservation.

Computational Complexity:The computational complexity of the median filter depends on the size of the sliding window or kernel. As the window size increases, the number of pixel comparisons and sorting operations also grows, leading to higher computational overhead. For larger images and large window sizes, the median filter can become computationally intensive, impacting real-time or resource-constrained applications. Researchers and practitioners often explore optimizations and parallelization techniques to speed up the filtering process without compromising the quality of results.

Noise Reduction Effectiveness:The median filter is particularly effective in handling salt-and-pepper noise and other impulsive noise types. Its ability to replace noisy pixel values with robust median estimates significantly reduces the impact of extreme noise values, resulting in clearer and cleaner images. However, the effectiveness of the median filter can vary based on the noise distribution and the choice of the window size. In scenarios where noise is predominantly Gaussian, other filtering techniques might offer better performance.

Window Size Selection:Selecting an appropriate window size is critical in balancing noise reduction and feature preservation. A smaller window size is effective in reducing localized noise but may not be sufficient for removing broader noise patterns. Conversely, a larger window size offers better noise suppression but can blur fine details and edges. Fine-tuning the window size based on the characteristics of the noise and the specific application is essential to achieve optimal results.

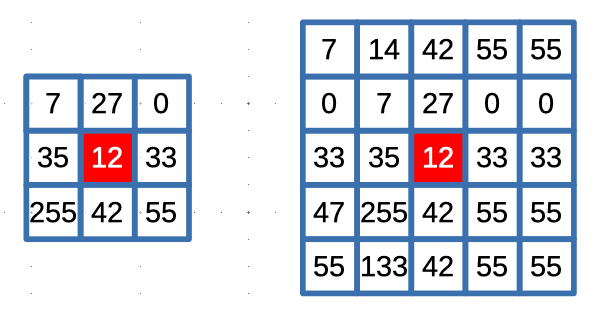
Boundary Effects: The median filter's operation near the image boundaries can be challenging since the sliding window extends beyond the image boundaries. This can result in incomplete neighborhoods, affecting the accuracy of the filtering process near the edges of the image. To address this issue, padding methods, such as zero-padding or mirroring, can be employed to extend the image boundaries artificially before applying the median filter.

Adaptive Median Filtering: In scenarios where noise characteristics vary across the image, adaptive median filters can be used. These filters dynamically adjust the window size based on the local pixel intensities. Adaptive median filters are particularly useful in handling images with varying noise levels or structures of different sizes. By tailoring the filtering process to specific image regions, adaptive median filters can achieve better noise reduction and feature preservation.

Combining Median Filter with Other Techniques: To further enhance noise reduction and image quality, the median filter can be combined with other filtering techniques or image processing methods. For instance, pre-processing an image with a Gaussian or bilateral filter can reduce Gaussian noise before applying the median filter to handle remaining impulsive noise. Such combinations allow for a synergistic approach that maximizes noise reduction while minimizing unwanted artifacts.

Advanced Median Filter Variants

While the basic median filter is a powerful technique for noise reduction in images, researchers have developed advanced variants that address specific challenges and noise scenarios more effectively. In this section, we explore some of these advanced median filter variants, each tailored to handle unique types of noise and improve overall filtering performance.

1. Adaptive Median Filter: The Adaptive Median Filter dynamically adjusts the window size based on the local pixel intensities within the sliding window. This variant is particularly useful in scenarios where the noise characteristics vary across the image. By employing a smaller window size in areas with low noise and a larger window size in regions with higher noise, the adaptive median filter can achieve better noise reduction while preserving details in both small and large structures. This approach is valuable when dealing with images containing both impulsive and continuous noise at different scales.

2. Weighted Median Filter: The Weighted Median Filter extends the concept of the traditional median filter by assigning weights to the pixels within the sliding window. The weights are usually determined based on pixel distances from the central pixel or their intensity values. By giving higher weights to pixels closer to the center or pixels with similar intensities, the weighted median filter can enhance noise reduction while considering the local structure of the image. This variant is particularly useful in scenarios where noise varies spatially and requires differential handling.

3. Vector Median Filter: The Vector Median Filter is an extension of the median filter designed for multi-dimensional data, such as color images or multi-spectral images. Instead of operating on individual pixel intensities, the vector median filter considers pixel vectors, including multiple components (e.g., RGB values). By computing the median of the pixel vectors in the sliding window, this variant effectively reduces noise in each channel while preserving color fidelity and feature details in the image.

4. Recursive Median Filter: The Recursive Median Filter is an efficient variant that reduces computational complexity by leveraging previously calculated median values. In a recursive approach, the median value for the current window is derived from the previously computed median value for the adjacent window. This method minimizes the number of pixel comparisons and sorting operations, making it more suitable for real-time and resource-constrained applications.

5. Directional Median Filter: The Directional Median Filter is designed to handle noise that follows specific directional patterns, commonly encountered in line-scanning or line-scan camera images. Instead of using a square sliding window, the directional median filter employs elongated or rectangular windows aligned along the direction of noise. This allows the filter to selectively suppress noise along specific directions while preserving features orthogonal to the noise pattern.

6. Adaptive Switching Median Filter: The Adaptive Switching Median Filter dynamically switches between median filtering and other filtering techniques based on the local noise characteristics. For example, it might switch to a mean or Gaussian filter when encountering uniform noise and revert to the median filter when impulsive noise is prevalent. This approach optimizes noise reduction while maintaining computational efficiency.

7. Non-Local Median Filter: The Non-Local Median Filter extends the concept of the median filter by considering similar patches from various locations in the image. By comparing the similarity between patches, this variant can identify and preserve important structures and textures while suppressing noise more effectively. Non-local approaches are beneficial when dealing with complex and heterogeneous noise patterns.

These advanced median filter variants showcase the adaptability and versatility of the median filter family in image processing. Each variant caters to specific noise scenarios and image characteristics, offering improved noise reduction and feature preservation in their respective domains.

Implementing the Median Filter

Implementing the median filter involves coding the necessary algorithms and data structures to apply the filtering operation to digital images. While the concept of the median filter is straightforward, the implementation details can vary based on factors such as programming language, image representation, and performance requirements. Below, we provide an C++ implementation

bool comparePixelsByRGB(const Pixel& a, const Pixel& b) {
    float sum_a = a.r + a.g + a.b;
    float sum_b = b.r + b.g + b.b;
    return sum_a < sum_b;
}

Pixel applyMedianFilterToPixel(Image& img, int row, int col, int filter_size) {
    std::vector<Pixel> values;

    // Collect pixel values in the local neighborhood
    for (int i = -filter_size / 2; i <= filter_size / 2; ++i) {
        for (int j = -filter_size / 2; j <= filter_size / 2; ++j) {
            int r = row + i;
            int c = col + j;

            // Check if the pixel is within bounds
            if (r >= 0 && r < img.height && c >= 0 && c < img.width) {
                values.push_back(img.at(r, c));
            }
        }
    }

    // Calculate the median
    int middle = values.size() / 2;
    std::nth_element(values.begin(), values.begin() + middle, values.end(), comparePixelsByRGB);
    return values[middle];
}

// Define a function to apply median filter to an RGB image
Image applyMedianFilterToImage(Image& image, int filter_size = 3) {
    int rows = image.height;
    int cols = image.width;

    Image filtered_image = image;

    for (int r = 0; r < rows; ++r) {
        for (int c = 0; c < cols; ++c) {
            filtered_image.at(r, c) = applyMedianFilterToPixel(image, r, c, filter_size);
        }
    }

    return filtered_image;
}

Explanation:

1. The comparePixelsByRGB function defines a custom comparator that compares two Pixel objects based on the sum of their RGB values. This is used to sort the pixels for the median calculation.
2. The applyMedianFilterToPixel function applies the median filter to a single pixel of an image at a specified row and column. It collects pixel values in a local neighborhood defined by the filter_size, calculates the median using std::nth_element and the custom comparator, and returns the median pixel.
3. The applyMedianFilterToImage function applies the median filter to an entire RGB image. It iterates over each pixel in the image and applies the median filter separately to each pixel using the applyMedianFilterToPixel function.

Testing and Validation:

To illustrate the efficacy of the median filter in mitigating various noise types, we conducted a series of tests using distinct noisy images. For each noisy image, we applied the median filter and scrutinized the outcomes.

Original image

Salt and pepper

The median filter exhibited commendable performance in addressing salt and pepper noise, effectively smoothing out the distortion.

Speckle noise

For speckle noise reduction, the median filter achieved a moderate level of success. While some noise reduction was evident, traces of graininess persisted in the filtered output.

Shot noise

Among the tested noise types, shot noise proved to be the most challenging for the median filter. Despite its efforts, the filter exhibited limited success in noise reduction, and discernible artifacts remained in the filtered result.

Gauss noise

When dealing with Gaussian noise, the median filter exhibited a relatively higher level of success in noise reduction. While some noise artifacts were still present, the filtered output displayed notable improvements.

Conclusion

In conclusion, the median filter stands as a powerful tool, fortifying image processing applications against the challenges posed by noise. By adopting best practices, optimizing parameters, and customizing the filter to specific noise scenarios, we can harness its potential to create clearer, more informative images, enriching our understanding and enabling better decision-making in the world of image analysis.

As technology continues to evolve, so does the significance of the median filter, as it remains a timeless solution in the quest for noise reduction, image enhancement, and feature preservation. Armed with this knowledge, let us continue to explore and innovate, pushing the boundaries of image processing and paving the way for new breakthroughs in computer vision, medical diagnostics, and beyond.