LeeCode: 96. Unique Binary Search Trees

The Problem

Given an integer n, return the number of structurally unique BST's (binary search trees) which has exactly n nodes of unique values from1ton.

Example

n = 3

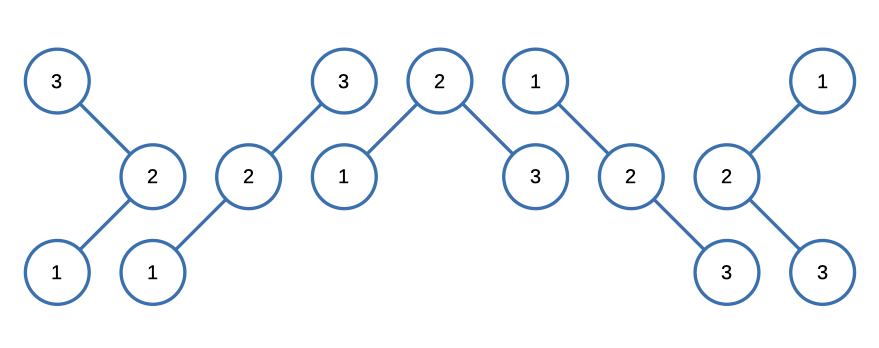
Input:  n = 3
Output: 5

Constraints:

• 1 <= n <= 19

The solution

We initially implemented the calculation of Catalan numbers using a recursive function. However, we encountered issues when dealing with sufficiently large numbers where the result exceeded the valid representation even for unsigned long long integers. As a result, we opted for an iterative approach to address this problem, and upon evaluating our solution on the LeetCode platform, we achieved the following outcome:

Here's the code that led us to this result.

int numTrees(int n) {
    int result = 1;

    for(int i = 0; i < n; ++i)
	    result *= (2.0 * (2.0 * i + 1)) / (i + 2 );

    return result;
}

Here's an explanation of the code step by step:

1. int numTrees(int n): This is the function declaration. It takes an integer n as its parameter, representing the number of distinct nodes for which we want to calculate the number of BSTs. It returns an integer representing the approximate number of BSTs.

2. int result = 1;: This initializes an integer variable result to 1. This variable will be used to accumulate the result of the calculation.

3. for(int i = 0; i < n; ++i): This is a for loop that iterates from i = 0 to i < n. In each iteration of the loop, it calculates a term in the formula for the Catalan number.

4. result *= (2.0 * (2.0 * i + 1)) / (i + 2 );: In each iteration of the loop, this line updates the result by multiplying it by a term. This term is calculated based on the simplified Catalan number formula:

• (2.0 * (2.0 * i + 1)) calculates the numerator, which involves doubling the value of i, adding 1, and then doubling the result again. This corresponds to the numerator of the formula.
• (i + 2) calculates the denominator, which involves adding 2 to the value of i. This corresponds to the denominator of the formula.The result of this calculation is then multiplied by the current value of result, effectively accumulating the product in the result variable.

5. After the loop has completed, the result variable contains the approximate number of BSTs that can be formed with n distinct nodes.

6. Finally, return result; returns this calculated result from the function.