LeetCode: 95. Unique Binary Search Trees II

The Problem

Given an integer n, return all the structurally unique BST's (binary search trees), which has exactly n nodes of unique values from1ton. Return the answer in any order.

Example

N = 3

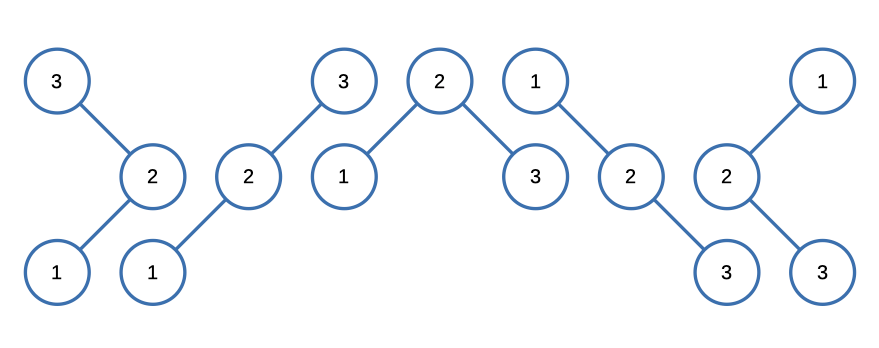
Input: n = 3
Output: [
	[1,null,2,null,3],
    [1,null,3,2],
    [2,1,3],
    [3,1,null,null,2],
    [3,2,null,1]
]

Constraints:

• 1 <= n <= 8

Solution

We opted for a recursive approach to tackle this problem, and upon evaluating our solution on the LeetCode platform, we achieved the following outcome:

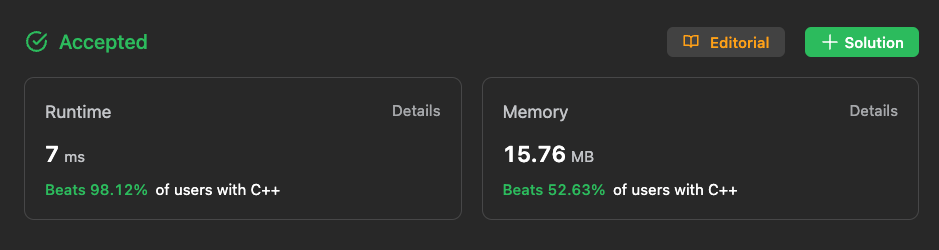
Here's the code that led us to this result.

vector<TreeNode*> generateTrees(int n) {
	return createTrees(1, n);
}

vector<TreeNode*> createTrees(int start, int end) {

    if (start > end) return { NULL };
    else if (start == end) return { new TreeNode(start) };

    vector<TreeNode*> result;

        for (int i = start; i <= end; ++i) {

        vector<TreeNode*> leftSubtrees = createTrees(start, i - 1);
        vector<TreeNode*> rightSubtrees = createTrees(i + 1, end);

            for (TreeNode* &leftTree : leftSubtrees) {
                for (TreeNode* &rightTree : rightSubtrees) {
                    TreeNode* root = new TreeNode(i);

                    root->left = leftTree;
                    root->right = rightTree;

                    result.push_back(root);
                }
        }
    }

    return result;
}

Let's break down the code step by step:

1. The primary function generateTrees(int n) is a public function that takes the total number of nodes n as input. It initializes the process by calling the private createTrees function with the range [1, n] and returns the result.

2. The private function createTrees(int start, int end) is the heart of the algorithm. It generates all possible unique BSTs for nodes within the range [start, end].

• If start is greater than end, it means there are no nodes in the current range, so it returns a vector with a single element containing NULL to represent an empty tree.
• If start is equal to end, it means there is only one node in the range, and it creates a tree with that single node and returns it as a vector with a single element.

Otherwise, there is more than one node in the range. The code enters a loop from start to end, representing each node as the root of a potential BST.

• It recursively calls createTrees to generate all possible left subtrees for the current node (nodes less than i) and all possible right subtrees (nodes greater than i).
• It then combines each left subtree with each right subtree, attaching the current node as the root, and adds the resulting tree to the result vector.

3. Finally, the function returns the result vector, which contains all possible BSTs that can be formed using nodes in the range [start, end].