LeetCode: 94. Binary Tree Inorder Traversal

The Problem

Given the root of a binary tree, return the inorder traversal of its nodes' values.

Example

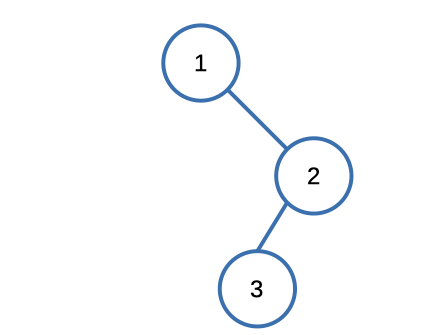
Input:  [1,null,2,3]
Output: [1,3,2]

Solution

We opted for a recursive approach to tackle this problem, and upon evaluating our solution on the LeetCode platform, we achieved the following outcome:

Here's the code that led us to this result.

void inorder(TreeNode* node, vector<int> &ans){
    if (node == NULL) return;

    inorder(node->left, ans);
    ans.push_back(node->val);

    inorder(node->right, ans);
}

vector<int> inorderTraversal(TreeNode* root) {
    vector<int> ans;
    inorder(root, ans);
    return ans;
}

Let's break down this code step by step:

Function Declaration: The code defines a function named inorder that takes two parameters:

• node: This is a pointer to a TreeNode object, representing a node in a binary tree.
• ans: This is a reference to a vector of integers (vector<int>) where we will store the values of the tree nodes in a specific order.

1. Base Case: The first line inside the inorder function checks if the node is NULL, which means there's no node at that position. If this is the case, the function immediately returns. This is a stopping condition for the recursion and prevents the function from going further down the tree when there's no more node to process.
2. Recursion - Left Subtree: If the node is not NULL, the function continues to execute. The next line calls the inorder function recursively on the left child of the current node. This is where the magic of the tree traversal happens. It's like saying, "Hey function, go to the left child of the current node and repeat the same process."
3. Collect Value: After processing the left subtree (which includes traversing all its left children), the code line ans.push_back(node->val) is executed. This line adds the value of the current node to the end of the ans vector. This is crucial because, in an inorder traversal, the left subtree is processed first, then the current node, and finally the right subtree. This sequence ensures that the values are collected in the correct order.
4. Recursion - Right Subtree: Finally, the last line of the function calls the inorder function recursively on the right child of the current node. This is similar to what was done for the left subtree. The function will go to the right child and repeat the same process: exploring its left subtree, collecting the value, and then exploring its right subtree.