LeetCode: 897. Increasing Order Search Tree

The Problem

Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.

Example

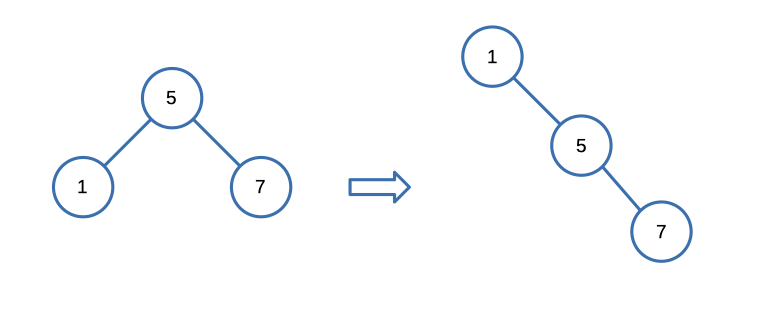
Input:  [5,1,7]
Output: [1,null,5,null,7]

Constraints:

• The number of nodes in the given tree will be in the range [1, 100].
• 0 <= Node.val <= 1000

Solution

We opted for a recursive approach to tackle this problem, and upon evaluating our solution on the LeetCode platform, we achieved the following outcome:

Here's the code that led us to this result.

TreeNode* increasingBST(TreeNode* root) {
    if(root == nullptr) return root;

    vector<TreeNode*> vec;
    increasingBST(root, vec);

    TreeNode* ans = vec.front();
    TreeNode* head = ans;

    ans->left = NULL;
    ans->right = NULL;

    for(int i = 1; i < vec.size(); ++i){
        head->right = vec[i];
        head = head->right;
        head->right = NULL;
        head->left = NULL;
    }

    return ans;
}

void increasingBST(TreeNode* root, vector<TreeNode*> &vec) {
    if(root == nullptr) return;

    increasingBST(root->left, vec);
    vec.push_back(root);
    increasingBST(root->right, vec);
}

Let's break it down step by step:

1. The goal of this code is to restructure a binary search tree to create a new tree where all the nodes are connected in increasing order.
2. The TreeNode structure likely represents a node in a binary tree, with properties like left and right representing the left and right child nodes.
3. The increasingBST function is a helper function that traverses the original tree (in-order traversal) and collects nodes in an increasing order in the vec vector.
4. The increasingBST function does this by recursively visiting the left subtree, adding the current node to the vec vector, and then visiting the right subtree.
5. The main increasingBST function is called with the root of the original tree and the vec vector as arguments. This will populate the vec vector with the nodes of the original tree in increasing order.
6. After the vec vector is populated, the code creates a new BST using the nodes from the vec vector. It starts by setting the first node in the vector as the ans node.
7. The loop then iterates through the remaining nodes in the vec vector and connects them to the ans node's right child. It updates the head node to the newly connected node after each iteration.
8. During each iteration, the code also removes any connections to the left or right children of the newly connected node, effectively creating a new right-leaning BST.
9. Finally, the ans node is returned, representing the root of the new BST with nodes connected in increasing order.