LeetCode: 69. Sqrt(x)

The Problem

Given a non-negative integer x, return the square root of x rounded down to the nearest integer. The returned integer should be non-negative as well.

You must not use any built-in exponent function or operator.

• For example, do not use pow(x, 0.5) in c++ or x ** 0.5 in python.

Examples:

1. Input: x = 4 Output: 2 Explanation: The square root of 4 is 2, so we return 2.

2. Input: x = 8 Output: 2 Explanation: The square root of 8 is 2.82842..., and since we round it down to the nearest integer, 2 is returned.

Constraints:

• 0 <= x <= 231 - 1

Solution

We opted for a simple approach using a while loop and the Newton's method to find root squares.

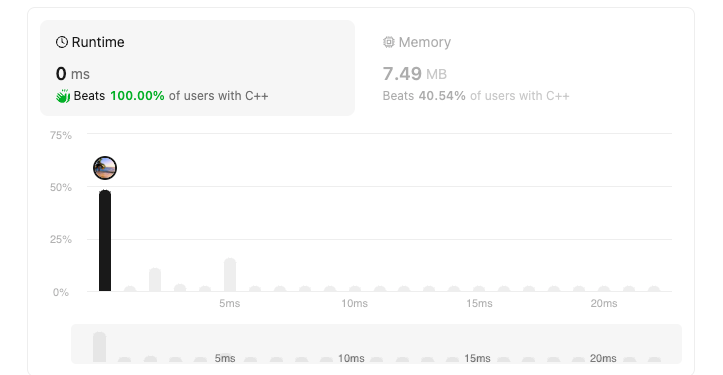
Here is the code that let us to that result

int mySqrt(int x) {
	
    if(x <= 1) return x;

	int ans = x / 2, temp;

	while(true){
		temp = (ans + x / ans) / 2;
		if (temp >= ans) {
			return ans;
		}
		ans = temp;
	}
	return ans;
}

Explanation

This function mySqrt calculates the integer square root of a given number x. Here's how it works:

1. The function first checks if the input x is less or equal to 1. If x is 0 or 1, the square root is simply x, so it returns x in this case.

2. If x is greater than 1, the function initializes a variable ans to x / 2. This is an initial guess for the square root of x.

3. The function enters a loop where it continually refines the guess for the square root until it converges to the correct value. Inside the loop:

• It calculates a new guess temp using the formula (ans + x / ans) / 2. This is a common method known as Newton's method for finding roots.
• If the new guess temp is greater than or equal to the current guess ans, it means the guess is converging, so it returns the current guess ans.
• If the new guess temp is smaller than the current guess ans, it updates the current guess ans to the new guess temp and continues the loop.

4. Once the loop exits, it returns the final value of ans, which is the integer square root of x.