LeetCode: 543. Diameter of Binary Tree

The Problem

Given the root of a binary tree, return the length of the diameter of the tree.

The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.

The length of a path between two nodes is represented by the number of edges between them.

Example

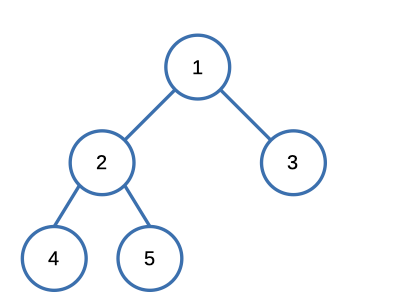
Input:  [1,2,3,4,5]
Output: 3
Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].

Solution

We opted for a recursive approach to tackle this problem, and upon evaluating our solution on the LeetCode platform, we achieved the following outcome:

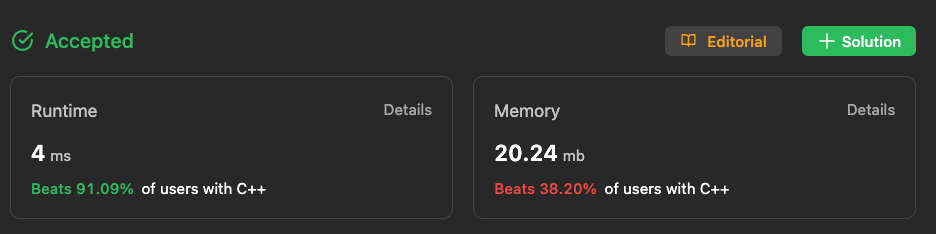
Here's the code that led us to this result.

int diameterOfBinaryTree(TreeNode* root) {
    int maxDiameter = 0;
    diameterOfBinaryTree(root, maxDiameter);
    return maxDiameter;
}

int diameterOfBinaryTree(TreeNode* root, int &maxDiameter) {
    if (root == nullptr) return 0;

    int left_h = diameterOfBinaryTree(root->left, maxDiameter);
    int right_h = diameterOfBinaryTree(root->right, maxDiameter);

    maxDiameter = max(maxDiameter, left_h + right_h);

    return 1 + max(left_h, right_h);
}

Here's how it works:

1. if (root == nullptr) return 0;: If the current node root is null (empty), we return 0, indicating the height of an empty subtree.
2. int left_h = diameterOfBinaryTree(root->left, maxDiameter);: We recursively call the function on the left subtree and store the returned height in left_h.
3. int right_h = diameterOfBinaryTree(root->right, maxDiameter);: Similarly, we do the same for the right subtree and store the returned height in right_h.
4. maxDiameter = max(maxDiameter, left_h + right_h);: We update the maxDiameter if the sum of the heights of the left and right subtrees is larger than the current maxDiameter. This accounts for paths that pass through the root.
5. return 1 + max(left_h, right_h);: We return the height of the current subtree. The 1 + is added because we're counting the root node itself as part of the height.

In summary, we traverse the binary tree in a recursive manner, calculate the heights of subtrees, and update the maximum diameter whenever a longer path is found.