LeetCode: 437. Path Sum III

The Problem

Given the root of a binary tree and an integer targetSum, return the number of paths where the sum of the values along the path equals targetSum.

The path does not need to start or end at the root or a leaf, but it must go downwards (i.e., traveling only from parent nodes to child nodes).

Example

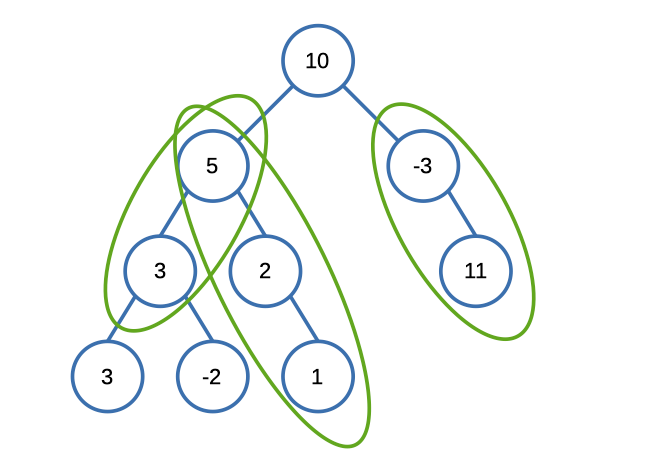
Input: root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
Output: 3
Explanation: The paths that sum to 8 are shown.

Constraints:

• The number of nodes in the tree is in the range [0, 1000].
• -109 <= Node.val <= 109
• -1000 <= targetSum <= 1000

Solution

We opted for a recursive approach to tackle this problem, and upon evaluating our solution on the LeetCode platform, we achieved the following outcome:

Here's the code that led us to this result.

int pathSum(TreeNode* root, int targetSum) {
    unordered_map<long, int> sum_paths;
    sum_paths[0] = 1;
    int count = 0;
    pathSumHelper( root, sum_paths, 0, targetSum, count );
    return count;
}

void pathSumHelper(
	TreeNode *&root, 
	unordered_map<long, int> &sum_paths,
	long currentSum,
	int &targetSum, int &count
) {
	if (root == NULL) return;
	currentSum = currentSum + root->val;
	count = count + sum_paths[currentSum - targetSum];

	++sum_paths[currentSum];
	pathSumHelper( root->left, sum_paths, currentSum, targetSum, count );
	pathSumHelper( root->right, sum_paths, currentSum, targetSum, count );
	--sum_paths[currentSum];
}

It uses a depth-first search (DFS) approach with a map to keep track of cumulative sums for optimizing.

1. int pathSum(TreeNode* root, int targetSum): This is the main function that initiates the counting of paths. It uses an unordered map called sum_paths to keep track of cumulative sums along paths. The function pathSumHelper is called to perform the actual traversal and counting.

void pathSumHelper(...): This is a helper function that performs the DFS traversal. It takes the current root node, sum_paths, currentSum, targetSum, and count as arguments.

• If the root is NULL, it means we've reached the end of a path, and it returns.
• It updates the currentSum by adding the value of the current node to it.
• It increments count by the number of times the value currentSum - targetSum has been seen in sum_paths. This indicates how many times the sum matches the targetSum.
• It increments the count of currentSum in the sum_paths map.
• It recursively calls pathSumHelper for the left and right child nodes of the current node.
• It decrements the count of currentSum in sum_paths to backtrack for other paths.