LeetCode: 337. House Robber III

The Problem

The thief has found himself a new place for his thievery again. There is only one entrance to this area, called root.

Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that all houses in this place form a binary tree. It will automatically contact the police if two directly-linked houses were broken into on the same night.

Given the root of the binary tree, return the maximum amount of money the thief can rob without alerting the police.

Example

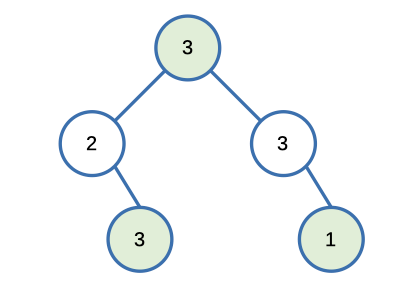
Input:  [3,2,3,null,3,null,1]
Output: 7
Explanation: Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• 0 <= Node.val <= 104

Solution

We opted for a recursive approach to tackle this problem, and upon evaluating our solution on the LeetCode platform, we achieved the following outcome:

Here's the code that led us to this result.

int rob(TreeNode* root) {
    pair<int, int> ans = robHelper(root);
    return max(ans.first, ans.second);
}

pair<int, int> robHelper(TreeNode *&root) {
    if (root == NULL) return { 0, 0 };

    pair<int, int> left = robHelper(root->left);
    pair<int, int> right = robHelper(root->right);

    int notRobbed = 
	    max( left.first,  left.second) +
    	max(right.first, right.second);

	int robbed = root->val + left.first + right.first;
    
    return pair<int, int>{notRobbed, robbed};
}

Here's a simplified explanation:

1. int rob(TreeNode* root): This is the main function that initiates the calculation. It calls the robHelper function to perform the actual computation. It returns the maximum amount of money that can be robbed from the binary tree.

2. pair<int, int> robHelper(TreeNode *&root): This helper function calculates the maximum amount that can be robbed from the current subtree rooted at root. It returns a pair of values: {notRobbed, robbed}.

• If the root is NULL, it means there are no houses to rob in this subtree, so it returns {0, 0}.
• It recursively calls robHelper for the left and right child nodes and gets their results as left and right.
• It calculates two values: notRobbed and robbed.
• notRobbed is the maximum value when the current house is not robbed. It is calculated by taking the maximum of the sum of not robbing the left child and not robbing the right child.
• robbed is the maximum value when the current house is robbed. It is calculated by adding the value of the current house, the notRobbed value of the left child, and the notRobbed value of the right child.
• It returns the pair {notRobbed, robbed} for the current subtree.