LeetCode: 230. Kth Smallest Element in a BST

The Problem

Given the root of a binary search tree, and an integer k, return thekthsmallest value (1-indexed) of all the values of the nodes in the tree.

Example

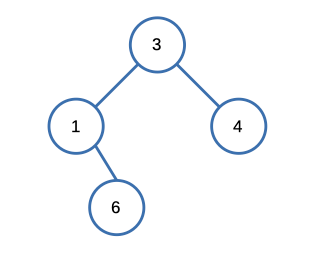
Input:  [3,1,4,null,2], k = 1
Output: 1

Constraints:

• The number of nodes in the tree is n.
• 1 <= k <= n <= 104
• 0 <= Node.val <= 104

Solution

We opted for a recursive approach to tackle this problem, and upon evaluating our solution on the LeetCode platform, we achieved the following outcome:

Here's the code that led us to this result.

int kthSmallest(TreeNode* root, int k) {
    int ans = 0;
    kthSmallestHelper(root, k, ans);
    return ans;
}

void kthSmallestHelper(TreeNode *&root, int &k, int &ans) {

	if (root == NULL) return;

	kthSmallestHelper(root->left, k, ans);
    --k;
    if(k == 0) {
    	ans = root->val;
	    return;
    } 
    kthSmallestHelper(root->right, k, ans);
}

Here's how the code works step by step:

1. The kthSmallest function is the entry point. It initializes a variable ans to store the result, which will be the kth smallest element. It then calls the kthSmallestHelper function with the root node, k, and ans as arguments.
2. The kthSmallestHelper function is a recursive helper function that navigates the BST to find the kth smallest element. It takes three parameters: a reference to the current root node (TreeNode *&root), a reference to the remaining number of elements to find (int &k), and a reference to store the result (int &ans).
3. The function first checks if the current node root is NULL. If it is, it means we have reached a leaf node or a null child, so there's nothing to do, and the function returns.
4. The function then recursively calls itself on the left subtree (root->left). This is done to traverse the BST in an in-order fashion, which ensures that we visit the elements in ascending order.
5. After the left subtree has been processed, the function decrements k by 1. This represents the number of remaining elements to find.
6. Next, the function checks if k has reached 0. If k is equal to 0, it means we have found the kth smallest element. In this case, it sets ans to the value of the current node's value (root->val) and returns. This termination condition ensures that we stop the traversal as soon as we find the kth smallest element.
7. If k is still greater than 0 after decrementing, it means we haven't found the kth smallest element yet, so the function continues the traversal by recursively calling itself on the right subtree (root->right).

The in-order traversal of the BST and the decrementing of k ensure that we find the kth smallest element in the BST efficiently. Once the kth smallest element is found, it is stored in the ans variable, which is returned by the kthSmallest function as the final result.