LeetCode: 226. Invert binary tree

The problem:

Given the root of a binary tree, invert the tree, and return its root.

Example

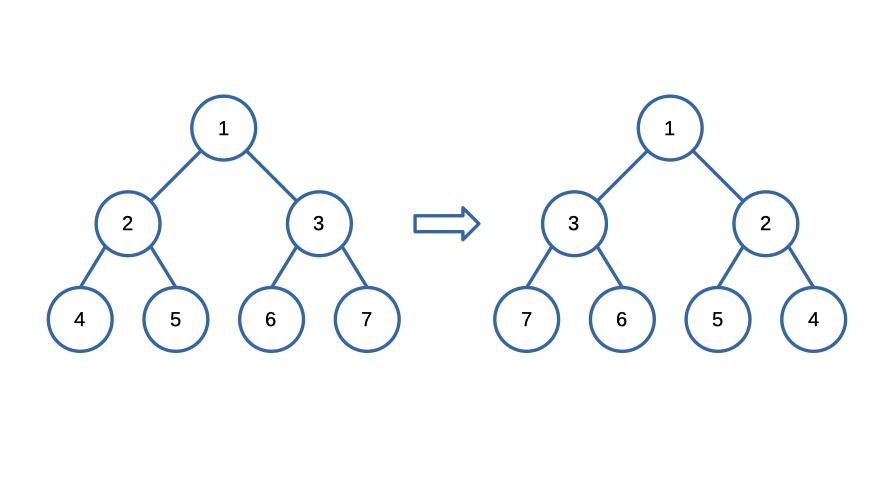
Input:  [1, 2, 3, 4, 5, 6, 7]
Output: [1, 3, 2, 7, 6, 5, 4]

Solution

We opted for a recursive approach to tackle this problem, and upon evaluating our solution on the LeetCode platform, we achieved the following outcome:

Here's the code that led us to this result.

TreeNode* invertTree(TreeNode* root) {

	// Base case: If the node is null, return nullptr.
    if(!root) return nullptr; 

	// Store the childs temporarily.
    TreeNode *tempL = root->left;
    TreeNode *tempR = root->right;

    // Swap the childs
    root->left = tempR;
    root->right = tempL;

	// Recursively invert the left and right subtrees.
    invertTree(root->left);
    invertTree(root->right);
    
    // Return the root of the inverted tree.
    return root;
}

Recursion is used to traverse the binary tree, swapping the left and right children at each node and recursively applying the same inversion operation to its left and right subtrees. This recursive pattern allows the function to efficiently invert the entire tree without explicitly needing to keep track of each level or iteration

Let's break the solution step by step:

Base Case:

• The function starts by checking if the current node root is null. If it is, it means that we have reached a leaf node or an empty subtree. In such cases, there's nothing to invert, so we return nullptr.

Swapping Children:

• If the current node root is not null (i.e., we are at a non-leaf node), we proceed to swap its left and right children.
• A temporary pointer tempL and tempR is used to store the current childs temporarily.
• The code then swaps the positions of the left and right children of the current node, effectively inverting their positions.

Recursion:

• After swapping the children, the function recursively calls invertTree on both the left and right subtrees.
• This step ensures that the inversion operation is applied to all nodes in the binary tree, from the current node down to the leaves.

Returning the Root:

• Finally, the function returns the root of the inverted tree. This is essential because after the swaps and recursive calls, the structure of the tree has been modified, and we want to ensure that the topmost node of the tree remains the same.

Coding Tips:

For beginners, the idea of using recursion to flip a binary tree might seem a bit mysterious, almost like unraveling a puzzle with a touch of magic, but fear not! Here are some invaluable coding tips to guide you on your journey towards mastering this challenge:

1. Start with Base Cases:When dealing with recursive functions, it's essential to define your base cases first. In the context of inverting a binary tree, the base case is when the current node is null (empty). Handling base cases properly ensures your recursion terminates correctly.
2. Use Temporary Variables for Swapping:The act of swapping left and right children at a node is a central operation. Utilize temporary variables to safely swap the children without losing references. This avoids unintended changes and maintains the integrity of the tree.
3. Harness the Power of Recursion:Embrace the elegance of recursion by treating subtrees as smaller versions of the same problem. Focus on inverting a single node, then delegate the inversion of its left and right subtrees to recursive calls. Remember, the magic happens step by step.
4. Check Each Node Individually:In your recursive calls, remember that each node should be treated as an independent entity. Your function should only concern itself with inverting the specific node it's processing, while the recursive calls handle the rest.
5. Mind the Order of Operations:When calling invertTree(root->left) and invertTree(root->right), ensure that the inversion happens before any further modifications to the tree structure. This sequence guarantees the correct inversion and maintains the integrity of the tree.
6. Test Extensively:Leverage a variety of test cases to validate your solution thoroughly. Test with different tree structures, including unbalanced and degenerate trees, to ensure your code handles all scenarios correctly.
7. Use Debugger and Print Statements:If you encounter unexpected behavior, consider using print statements or a debugger to inspect the state of variables and the flow of execution. This can help pinpoint issues in your code and aid in debugging.
8. Watch Out for Null Pointers:Since you're dealing with pointers or references in tree nodes, ensure that you handle null pointers appropriately to avoid runtime errors. Always check if a node exists before accessing its properties.
9. Maintain Clean Code:As you code, keep your logic clear and organized. Use meaningful variable names, add comments to explain complex parts of your solution, and aim for a code structure that's easy to read and understand.
10. Iterate and Refine:Don't hesitate to iterate on your solution. Try different approaches, optimize your code, and refine your algorithm. Learning from each iteration will enhance your problem-solving skills.

By heeding these coding tips, you'll be well-prepared to tackle the challenge of inverting binary trees and navigate the intricate paths of recursion with confidence. Remember, the journey is as important as the destination, and each step brings you closer to mastering the art of binary tree manipulation!

Remember, coding is about exploration, experimentation, and continuous improvement. The path to mastery is paved with determination, persistence, and a sprinkle of coding magic. Whether you're just starting out or a seasoned coder, you have the potential to create extraordinary things.

So, what are you waiting for? Grab your keyboard, ignite your passion, and let the coding adventure begin! Share your code, share your thoughts, and be a part of this dynamic coding community