LeetCode: 222. Count Complete Tree Nodes

The problem

Given the root of a complete binary tree, return the number of the nodes in the tree.

According to Wikipedia, every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.

Design an algorithm that runs in less than O(n) time complexity.

Example

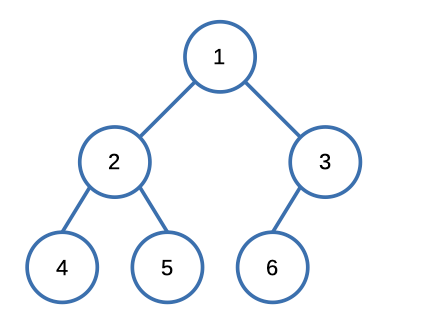
Input:  [1,2,3,4,5,6] 
Output: 6

Solution

We opted for a recursive approach to tackle this problem, and upon evaluating our solution on the LeetCode platform, we achieved the following outcome:

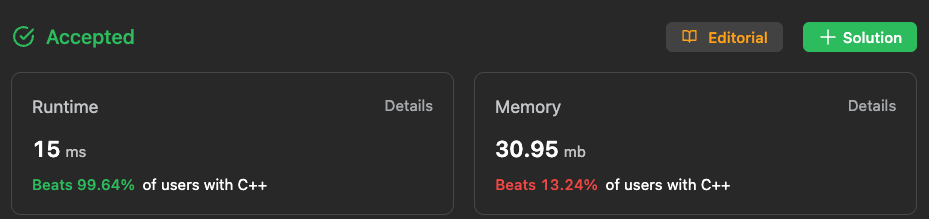
Here's the code that led us to this result.

int countNodes(TreeNode* root) {
    if (!root) return 0;
    TreeNode *left = root->left;
    TreeNode *right = root->right;
    return 1 + countNodes(left) + countNodes(right);
}

Let's break down the code step by step:

int countNodes(TreeNode* root) :

• This line declares the function countNodes that takes a pointer to a TreeNode called root as an argument.
• The function is expected to return an integer (int) representing the count of nodes in the binary tree.

if (!root) return 0;:

• This line is a conditional statement that checks whether the root pointer is pointing to a valid TreeNode (i.e., not null).
• If the root pointer is null (which means the tree is empty or we've reached the end of a branch), the function returns 0 to indicate that there are no nodes to count.

TreeNode *left = root->left; and TreeNode *right = root->right;:

• These lines create two new pointers, left and right, which point to the left and right children of the current root node, respectively.
• These pointers will be used to recursively traverse the left and right subtrees of the binary tree.

return 1 + countNodes(left) + countNodes(right);:

• This line is the core of the recursive function.
• It returns the count of nodes in the binary tree rooted at root.
• The count is calculated as follows:
• 1 is added to account for the current node.
• countNodes(left) is a recursive call to the countNodes function on the left subtree. This counts all nodes in the left subtree.
• countNodes(right) is a recursive call to the countNodes function on the right subtree. This counts all nodes in the right subtree.
• The function keeps breaking down the problem into smaller subproblems (left and right subtrees) until it reaches the base case (when a null node is encountered), at which point it starts returning values and building up the final count.

In summary, this code uses recursion to traverse a binary tree and count the total number of nodes in it. It starts from the root node and adds the count of nodes in the left and right subtrees, along with the current node, to calculate the total count.