LeetCode: 173. Binary Search Tree Iterator

The Problem

Implement the BSTIterator class that represents an iterator over the in-order traversal of a binary search tree (BST):

• BSTIterator(TreeNode root) Initializes an object of the BSTIterator class. The root of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
• boolean hasNext() Returns true if there exists a number in the traversal to the right of the pointer, otherwise returns false.
• int next() Moves the pointer to the right, then returns the number at the pointer.

Notice that by initializing the pointer to a non-existent smallest number, the first call to next() will return the smallest element in the BST.

You may assume that next() calls will always be valid. That is, there will be at least a next number in the in-order traversal when next() is called.

Example

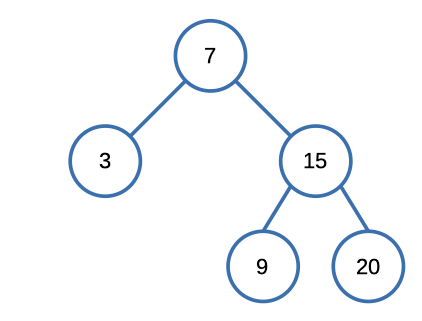
Input
["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
Output
[null, 3, 7, true, 9, true, 15, true, 20, false]

Explanation
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next();    // return 3
bSTIterator.next();    // return 7
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 9
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 15
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 20
bSTIterator.hasNext(); // return False

Constraints:

• The number of nodes in the tree is in the range [1, 105].
• 0 <= Node.val <= 106
• At most 105 calls will be made to hasNext, and next.

Solution

We opted for a recursive approach to tackle this problem, and upon evaluating our solution on the LeetCode platform, we achieved the following outcome:

Here's the code that led us to this result.

class BSTIterator {
    queue<int> nodes;

public:
    BSTIterator(TreeNode* root) {
        nodes.push(-1);
        fillNodes(root);
    }
    
    int next() {
        nodes.pop();
        return nodes.front();
    }
    
    bool hasNext() {
        return  nodes.size() > 1;
    }
    
    void fillNodes(TreeNode* root) {
        if (root == NULL) return;
        fillNodes(root->left);
        nodes.push(root->val);
        fillNodes(root->right);
    }

};

Let's break down this code step by step:

1. class BSTIterator {: This line declares the start of a class definition named BSTIterator. This class will be responsible for iterating through the BST.

2. queue<int> nodes;: It declares a queue named nodes. In this queue, we will store the values of the BST nodes in in-order.

3. BSTIterator(TreeNode* root) {: This is the constructor of the BSTIterator class. It takes a pointer to the root of the BST as an argument.

• nodes.push(-1);: to initialized to a non-existent number smaller than any element in the BST
• fillNodes(root);: It then calls the fillNodes function to populate the nodes queue with values from the BST.

4. int next() {: used to get the next value in the BST.

• nodes.pop();: It removes the first element from the nodes queue.
• return nodes.front();: It returns the new front element of the queue, which will be the next smallest value in the BST.

5. bool hasNext() {: This is a member function named hasNext. It checks if there are more elements to iterate over.

• return nodes.size() > 1;: It returns true if the size of the nodes queue is greater than 1, meaning there are more elements to iterate. The extra -1 placeholder ensures this condition works correctly.

5. void fillNodes(TreeNode* root) {: This is a member function named fillNodes. It recursively populates the nodes queue with BST values.

• if (root == NULL) return;: If the current node is NULL (empty), it returns and does nothing.
• fillNodes(root->left);: It recursively calls fillNodes on the left subtree of the current node.
• nodes.push(root->val);: It pushes the value of the current node into the nodes queue. This is where the values are sorted in ascending order.
• fillNodes(root->right);: It recursively calls fillNodes on the right subtree of the current node.