LeetCode: 145. Binary Tree Postorder Traversal

The problem

Given the root of a binary tree, return the postorder traversal of its nodes' values.

Example

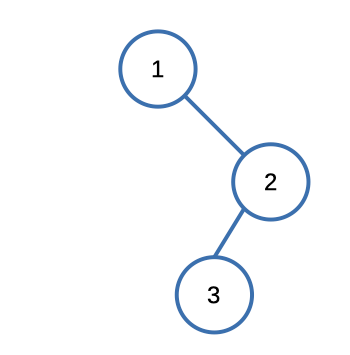
Input:  [1,null,2,3]
Output: [3,2,1]

Understanding the problem

Tree traversal is a fundamental technique in computer science, enabling us to explore the nodes of a tree-like data structure in a specific order. Postorder tree traversal is one such method that has its unique advantages. In this blog post, we'll take a deep dive into postorder traversal, accompanied by a clear and concise C++ code example.

Postorder Tree Traversal: In postorder traversal, we traverse a binary tree in the following order: left subtree, right subtree, root node. This order is particularly useful when we need to process a tree's nodes from the bottom up, such as when deallocating memory or performing mathematical operations.

Solution

We opted for a recursive approach to tackle this problem, and upon evaluating our solution on the LeetCode platform, we achieved the following outcome.

Here's the code that led us to this result.

vector<int> postorderTraversal(TreeNode* root) {
    vector<int> ans;
    postOrderNode(ans, root);
    return ans;
}

void postOrderNode(vector<int> &arr, TreeNode *node){
    if(node == nullptr) return;

    postOrderNode(arr, node->left);
    postOrderNode(arr, node->right);
    
    arr.push_back(node->val);
}

Understanding the solution, Postorder Tree Traversal in C++

The postorderTraversal function initiates the postorder traversal process. It takes a single argument, root, representing the root node of the binary tree. The function creates an empty vector called ans, which will store the values of the tree nodes in postorder traversal order.

The postOrderNode function, a helper function, executes the actual postorder traversal. It takes two parameters: a reference to the vector arr and a pointer to a TreeNode named node.

• If the current node is nullptr, indicating the end of a branch or subtree, the function returns, effectively concluding the traversal for that branch.
• If the node is not null, the function recursively calls postOrderNode on the left subtree (node->left) and the right subtree (node->right). This ensures that we traverse the subtrees before processing the current node.
• Finally, the value of the current node (node->val) is added to the end of the arr vector. This captures the bottom-up traversal order characteristic of postorder traversal.