LeetCode: 109. Convert Sorted List to Binary Search Tree

The Problem

Given the head of a singly linked list where elements are sorted in ascending order, convert it to a height-balanced binary search tree.

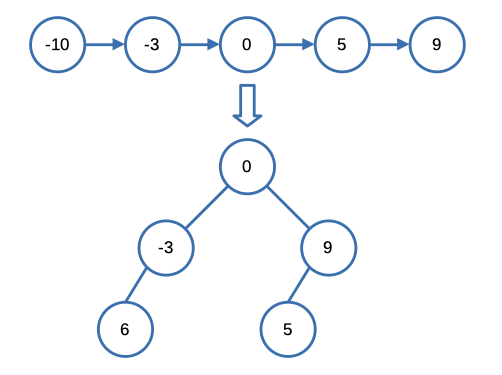
Input: head = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: One possible answer is [0,-3,9,-10,null,5], which represents the shown height balanced BST.

Constraints:

• The number of nodes in head is in the range [0, 2 * 104].
• -105 <= Node.val <= 105

Solution

We opted for a recursive approach to tackle this problem, and upon evaluating our solution on the LeetCode platform, we achieved the following outcome:

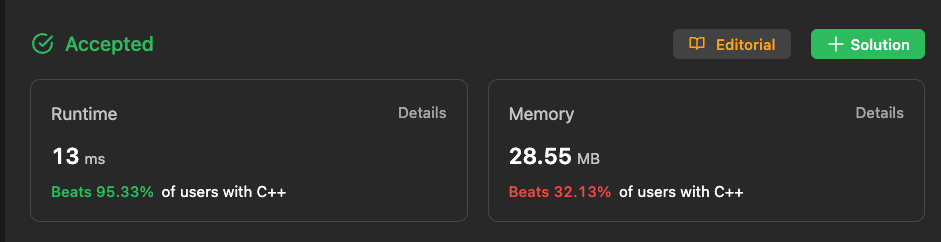
Here's the code that led us to this result.

TreeNode* sortedListToBST(ListNode* head) {
    if (head == nullptr) return nullptr;

    if (head->next == nullptr) return new TreeNode(head->val);

    ListNode *slow = head, *fast = head, *prev = nullptr;

    while( fast != nullptr && fast->next != nullptr) {
        prev = slow;
        slow = slow->next;
        fast = fast->next->next;
    }

    if (prev != nullptr) prev->next = nullptr;

    TreeNode *node = new TreeNode(slow->val);
    node->left = sortedListToBST(head);
    node->right = sortedListToBST(slow->next);

    return node;
}

Let me break it down step by step:

Base Cases:

• If the list is empty (head is nullptr), it returns an empty tree (nullptr).
• If the list has only one element (head->next is nullptr), it creates a tree with that element as the root and returns it.

Finding the Middle Node:

• It uses two pointers, slow and fast, to find the middle node of the list. slow moves one step at a time, and fast moves two steps at a time.
• While they move through the list, prev keeps track of the node just before slow. This is important for splitting the list.

Splitting the List:

• When the loop finishes, prev points to the node just before the middle node (slow). The code disconnects the list at this point by setting prev->next to nullptr. This separates the list into two halves.

Creating the Tree Node:

• It creates a new tree node (node) with the value of the middle node (slow->val). This node becomes the root of the tree.

Recursion:

• It calls itself recursively to construct the left and right subtrees:
• The left subtree is constructed from the elements before the middle node (recursively calling sortedListToBST(head)).
• The right subtree is constructed from the elements after the middle node (recursively calling sortedListToBST(slow->next)).

Returning the Root Node:

• The function returns the node, which is the root of the balanced binary search tree that it created from the sorted linked list.