LeetCode: 106. Construct Binary Tree from Inorder and Postorder Traversal

The Problem

Given two integer arrays inorder and postorder where inorder is the inorder traversal of a binary tree and postorder is the postorder traversal of the same tree, construct and return the binary tree.

Example

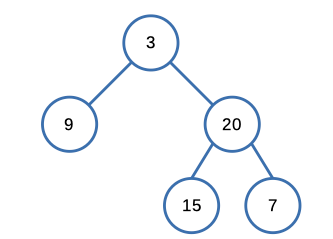
Input:  inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
Output: [3,9,20,null,null,15,7]

Constraints:

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder and postorder consist of unique values.
• Each value of postorder also appears in inorder.
• inorder is guaranteed to be the inorder traversal of the tree.
• postorder is guaranteed to be the postorder traversal of the tree.

Solution

We opted for a recursive approach to tackle this problem, and upon evaluating our solution on the LeetCode platform, we achieved the following outcome:

Here's the code that led us to this result.

TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
    unordered_map<int, int> inorderIndexMap;

    for (int i = 0; i < inorder.size(); ++i) 
	    inorderIndexMap[inorder[i]] = i;

    int postorderIndex = inorder.size() - 1;

    return buildTreeHelper(
    	postorder, inorder, 
	    postorderIndex, 
    	0, inorder.size() - 1,
	    inorderIndexMap
    );
}

TreeNode* buildTreeHelper(
	vector<int>& postorder, vector<int>& inorder, 
	int& postorderIndex, 
	int left, int right,
	unordered_map<int, int>& inorderIndexMap
) {

    if (left > right) return nullptr;

    int rootValue = postorder[postorderIndex];
    TreeNode* root = new TreeNode(rootValue);
    int inorderIndex = inorderIndexMap[rootValue];

    --postorderIndex;

    root->right = buildTreeHelper(
        postorder, inorder, 
        postorderIndex, 
        inorderIndex + 1, right,
        inorderIndexMap
    );

    root->left = buildTreeHelper(
        postorder, inorder, 
        postorderIndex, 
        left, inorderIndex - 1,
        inorderIndexMap
    );

    return root;
}

Let's break down this code step by step.

First, let's define a few key concepts:

• Inorder Traversal: The inorder traversal of a binary tree visits the nodes in the order "left, root, right." That is, it starts from the leftmost node, then goes to the root, and then to the right subtree.
• Postorder Traversal: The postorder traversal of a binary tree visits the nodes in the order "left, right, root." It starts from the leftmost node, then goes to the rightmost node, and finally visits the root.

Now, let's go through the code:

1. buildTree Function: This is the main function that constructs the binary tree. It takes two input vectors, inorder and postorder, representing the inorder and postorder traversals of the tree.
2. inorderIndexMap: An unordered_map is used to store the indices of values in the inorder vector. This map is created for efficient lookup of values during tree construction.
3. postorderIndex: This variable is initialized to the last index in the postorder vector. It keeps track of the current position in the postorder traversal.
4. Finally, the buildTreeHelper function is called with the postorder, inorder, postorderIndex, left index (0 initially), and right index (inorder.size() - 1 initially), along with the inorderIndexMap.

Now, let's look at the buildTreeHelper recursive function:

1. buildTreeHelper Recursive Function: This function is responsible for constructing a subtree of the binary tree.
2. Base Case: The function starts with a base case that checks if the left index exceeds the right index. If so, it returns nullptr to indicate an empty subtree.
3. Root Value: It retrieves the value of the root node from the postorder traversal. Since the postorder traversal processes nodes in the order "left, right, root," the root value is the last element at the current postorderIndex.
4. Creating the Root Node: A new TreeNode is created with the root value.
5. Finding Inorder Position: It finds the position of the root value in the inorder traversal using the inorderIndexMap. This allows us to determine the left and right subtrees in the inorder traversal.
6. Postorder Index Decrement: The postorderIndex is decremented to move to the previous value in the postorder traversal.
7. Recursive Calls: The function then recursively constructs the right subtree (postorder traversal) and the left subtree (postorder traversal) by adjusting the inorder indices accordingly.
8. Returning the Root: Finally, the function returns the root of the current subtree.