LeetCode: 102. Binary Tree Level Order Traversal

The Problem

Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).

Example

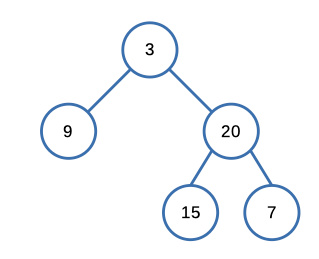
Input:  [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]

Constraints:

• The number of nodes in the tree is in the range [0, 2000].
• -1000 <= Node.val <= 1000

Solution

We opted for a recursive approach to tackle this problem, and upon evaluating our solution on the LeetCode platform, we achieved the following outcome:

Here's the code that led us to this result.

vector<vector<int>> levelOrder(TreeNode* root) {
    vector<vector<int>> ans;
    levelOrder(root, ans, 0);
    return ans;
}

void levelOrder(TreeNode *&root, vector<vector<int>> &ans, int level) {
    if(root == NULL) return;
    int nextLevel = level + 1;
    if(ans.size() < nextLevel) ans.resize(nextLevel);

    ans[level].push_back(root->val);

    levelOrder(root->left, ans, nextLevel);
    levelOrder(root->right, ans, nextLevel);
}

Here's a breakdown of the code:

1. The levelOrder function is the public entry point for the level-order traversal. It takes the binary tree's root node as input and initializes an empty vector of vectors (ans) to store the result.

2. It calls the private helper function levelOrder (the second function with the same name) to perform the traversal. The level argument is initially set to 0, indicating the root level.

3. In the private levelOrder function:

• It checks if the current node (root) is NULL. If it is, it returns immediately, as there's nothing to process for this node.
• It increments the nextLevel variable by 1 to represent the level below the current level.
• It checks if the ans vector has fewer levels than nextLevel. If so, it resizes ans to accommodate the new level.
• It adds the value of the current node (root->val) to the vector corresponding to the current level (ans[level]).
• It recursively calls the levelOrder function for the left and right children of the current node, passing nextLevel as the new level.

4. The levelOrder function is called initially from the public entry point with the root node and an empty ans vector. As the traversal progresses, the ans vector is filled with sub-vectors representing each level of the binary tree.

5. Finally, the ans vector, which now contains all the levels of the binary tree, is returned as the result of the level-order traversal.